정렬, 퀵 정렬

알고리즘 설명

<img alt="" src="https://static.podo-dev.com/blogs/images/2019/07/10/origin/PAPKSS181224235509.PNG" style="width:350px"/>

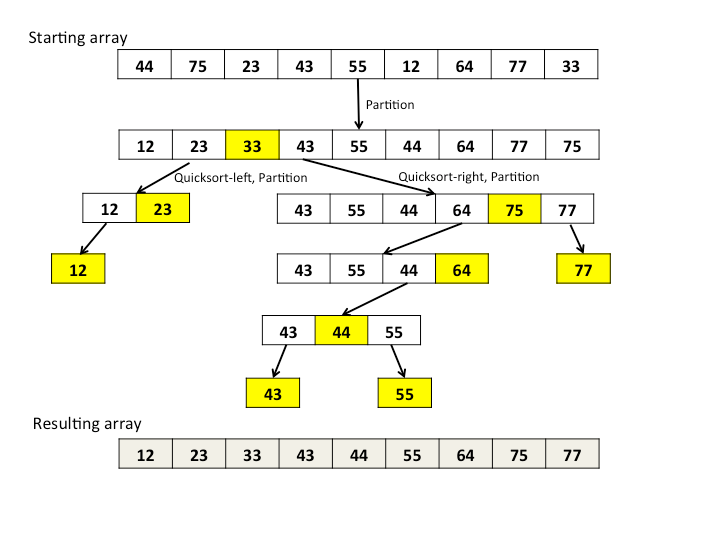
퀵 정렬은 분할정복 기법을 사용한다

피벗 A를 정한후, 왼쪽에는 피벗보다 작은값을, 오른쪽에는 피벗보다 큰 값을 둔다.

피벗 A의 왼쪽값에 대해 또 피벗B를 정해 왼쪽값에는 피벗B보다 작은 값을 오른쪽에는 피벗보다 큰 값을 둔다.

피벗 A의 오른쪽값에 대해 또 피벗C을 정해 왼쪽값에는 피벗C보다 작은 값을 오른쪽에는 피벗보다 큰 값을 둔다.

이 순회를 반복한다.

<br/>

복잡도

퀵정렬이 성능이 가장 좋을 때는 피벗을 중심으로 N/2개씩 분할이 반복 되었을때이다.

그럴 경우 log2N 단계가 생성되며, 최대 N번의 비교연산을 한다 그러므로 최선, 평균 복잡도 O(Nlog2N) 이다.

그러나 퀵정렬의 최악의 경우를 생각보자.

정렬이 역순으로 되어있고, 피벗은 항상 0 번째로 잡는 경우이다.

결국 N개의 단계가 생성되고 최대 N개의 비교를 한다.

따라서 최악의 경우 O(N^2)이다

<br/>

장단점

이름 그대로 빠른 것을 장점으로 가진다. 또한 추가적인 공간도 필요로 하지 않는다.

그러나 정렬된 리스트에 대해서는 성능이 떨어지며, 피벗을 중간값으로 사용함으로써 보완 할 수 있다.

<br/>

소스코드

package com.study.sort;

import java.util.Arrays;

public class QuickSort {
	public int sort(int[] arr, int start, int end) {
		int pivot = arr[start];
		int left = start + 1;
		int right = end;

		do{
			while (arr[left] < pivot &amp;&amp; left < end) {
				left++;
			}

			while (arr[right] > pivot &amp;&amp; right > start) {
				right--;
			}

			if (left < right) {
				int temp = arr[left];
				arr[left] = arr[right];
				arr[right] = temp;
			}

		}	while (left < right);

		int temp = arr[start];
		arr[start] = arr[right];
		arr[right] = temp;

		return right;
	}

	public void divide(int[] arr, int s, int e) {
		if (s < e) {
			int pivot = sort(arr, s, e);
			divide(arr, s, pivot - 1);
			divide(arr, pivot + 1, e);
		}
	}

	public static void main(String[] args) {
		int arr[] = { 5, 4, 3, 2, 1 };
		QuickSort quickSort = new QuickSort();
		quickSort.divide(arr, 0, arr.length - 1);
		System.out.print(Arrays.toString(arr));
	}
}
<br/>

<br/>